The following page contains miscellaneous technical information that may be of interest to the professional analyst.
The electron microprobe can provide quantitative chemical analysis for a wide variety of solid conducting and non-conducting samples including metals, alloys, glasses, minerals, single crystals, thin films and ceramics. For fully quantitative analysis it is generally essential that a 1/10 micron diamond or 1/20 micron colloidal silica polished flat surface be obtained on the sample.
Generally samples are prepared as round 25 mm thin-sections or grain mounts. Standard rectangular petrographic thin sections can also be prepared. The Cameca SX-51 electron microprobe can accommodate up to six 25 mm round mounts (including standards) or two petrographic thin-sections plus two 25 mm round samples (usually standard mounts).
The Department of Earth and Planetary Science has a dedicated petrographic laboratory staff facility for EPMA, SEM (scanning electron microscopy), XRF (x-ray fluorescence) and optical microscope thin section sample preparation. An experienced full time technical petrologist is available for consultation with and preparation of your samples. Please consult the technician, Tim Teague, for details regarding sample preparation.
Tim Teague
(510) 642-3514 (Voice)
(510) 643-9980 (FAX)
tteague@uclink2.berkeley.edu
Assume polypropylene density = 0.9 gm/cm3
Given a 100 mg/cm2 polypropylene film, calculate actual thickness in m (microns) :
![]() =
= ![]()
Convert to microns :
![]()
That is, 1.11 m
Therefore to convert mg/cm2 to microns, multiply by 0.0111 (1.11 divided by 100 mg/cm2)
For example, 30 mg/cm2 times 0.0111 = .333 m thickness
mg/cm2 |
m (microns) |
color |
10 |
0.111 |
straw |
15 |
0.166 |
dark blue |
20 |
0.222 |
pale yellow |
25 |
0.277 |
bright yellow |
30-35 |
0.333-0.388 |
orange-red |
35-40 |
0.388-0.444 |
violet-blue |
40-45 |
0.444-0.499 |
blue-green |
45-50 |
0.499-0.555 |
green-yellow |
50-55 |
0.555-0.611 |
yellow-red |
55-60 |
0.611-0.666 |
red-pink |
60-65 |
0.666-0.711 |
pale green to green |
65-70 |
0.711-0.777 |
green |
70-75 |
0.777-0.833 |
pale green to pale red |
Note, to convert m to path difference in mm (birefringence path length units) multiply by 2000 (103 times 2). For example, 1 m expressed as path difference in mm equals 2000 mm.
J. T. Armstrong and P. Buseck, "Quantitative Chemical Analysis of Individual Micro-particles using the Electron Microprobe" Anal. Chem. 47: 1975, p 2178
J. T. Armstrong, "Quantitative analysis of silicates and oxide minerals: Comparison of Monte-Carlo, ZAF and Phi-Rho-Z procedures," Microbeam Analysis--1988, p 239-246.
J. T. Armstrong, "Bence-Albee after 20 years: Review of the Accuracy of a-factor Correction Procedures for Oxide and Silicate Minerals," Microbeam Analysis--1988, p 469-476.
G. F. Bastin and H. J. M. Heijligers, "Quantitative Electron Probe Microanalysis of Carbon in Binary Carbides," Parts I and II, X-ray Spectr. 15: 135-150, 1986
W. A. Deer, R. A. Howie, J. Zussman, "An Introduction to the Rock Forming Minerals", Longman, Essex, London, 1966
J. J. Donovan and M. L. Rivers, "PRSUPR: A PC-Based Automation and Analysis Software Package for Wavelength-Dispersive Electron-Beam Microanalysis" Microbeam Analysis, 1990, p. 66-68
J. J. Donovan and V. C. Kress, "PRTASK: A PC-Based Acquisition and Analysis Software Package for Interfacing to the Tracor TASK Automation System" Microbeam Analysis, 1991, p. 351
J. J. Donovan, M. L. Rivers and J. T. Armstrong, "PRSUPR: Automation and Analysis Software for Wavelength Dispersive Electron-beam Microanalysis on a PC" in Am. Mineral., v. 77, 1992, p. 444
J. J. Donovan, D. A. Snyder and M. L. Rivers, "An Improved Interference Correction for Trace Element Analysis" Microbeam Analysis, 2: 23-28, 1993
J. J. Donovan and T. N. Tingle, "An Improved Mean Atomic Number Correction for Quantitative Microanalysis" in Journal of Microscopy, v. 2, 1, p. 1-7, 1996
J. Z. Frazer, ISM Report 67-29, 1967.
J.I. Goldstein, D.E. Newbury, P. Echlin, D.C. Joy, C. Fiori, E. Lifshin, "Scanning Electron Microscopy and X-ray Microanalysis", Plenum, New York, 1981
K. F. J. Heinrich, Proc. 11th ICXOM, 1987, p. 67.
K. F. J. Heinrich, "Mass Absorption Coefficients for Electron Probe Microanalysis" in Proc. 11th ICXOM 67: 1, 1982.
B. L. Henke, P. Lee, T. J. Tanaka, R. L. Shimabukuro and B. K. Fijikawa, Atomic Data Nucl. Data Tables 27, 1 (1982)
B. L. Henke and E. S. Ebisu, Adv. X-Ray Anal. 17, 150 (1974)
McQuire, A. V., Francis, C. A., Dyar, M. D., "Mineral standards for electron microprobe analysis of oxygen", Am. Mineral., 77, 1992, p. 1087-1091.
Nielsen, C. H. and Sigurdsson, H., "Quantitative methods for electron microprobe analysis of sodium in natural and synthetic glasses", Am. Mineral., 66, p. 547-552, 1981
J. L. Pouchou and F. M. A. Pichoir, "Determination of Mass Absorption Coefficients for Soft X-Rays by use of the Electron Microprobe" Microbeam Analysis, Ed. D. E. Newbury, San Francisco Press, 1988, p. 319-324.
Press et al. (1986) "Numerical Recipes: The Art of Scientific Computing", Cambridge University Press, 818 pp.
J. Ruste, J. Microsc. Spectrosc. Electron. 4, 123 (1979)
V. D. Scott and G. Love, "Quantitative Electron-Probe Microanalysis", Wiley & Sons, New York, 1983
K. G. Snetsinger, T. E. Bunch and K. Keil, "Electron Microprobe Analysis of Vanadium in the Presence of Titanium", Am. Mineral., v. 53, (1968) p. 1770-1773
E. W. White and G. G. Johnson, "X-Ray Emission and Absorption Edge Wavelengths and Interchange Settings for LiF Geared Curved Crystal Spectrometers", Pennsylvania State University Special Publication No. 1-70, 2nd Edition, (1979)
J. P. Willis, "Course on Theory and Practice of XRF Spectrometry", University of Western Ontario, Department of Geology, Course Notes, 1993
- EPMA is based on x-ray fluorescence (that is
emission as opposed to absorption spectroscopy)
- Utilizing x-rays between 0.1 and 100+ angstroms (between gamma
and ultra-violet)
- Technique is related to XRF (X-ray Fluorescence) and PIXE
(Particle Induced X-ray Emission)
Components (as distinguished from SEM, TEM, etc.) :
- high intensity electron beam (tungsten preferred for stability) of approx.1 - 200 nanoamps
- coaxial light optics (reflected and transmitted) at 300 - 400X)
- Energy Dispersive Spectrometry (EDS) is optional
- multiple wavelength dispersive spectrometers (WDS)
- high (> 40 degrees) x-ray take off angle for detectors
History :
- discovery of x-ray by Rontgen in 1895
- wave character confirmed by Von Laue
- first EPMA built by Starke in 1898 in Berlin (found backscatter intensity varies with Z)
- term "characteristic x-rays" was first used by Barkla and Sadler in 1909 but the physical origin of x-rays was not clear
- the Bohr atom explained the characteristic x-ray spectra
- Kaye (1909) built an cathode ray tube with an ionization chamber to detect x- rays
- first crystal spectrometer built by W. H. and W. L. Bragg interpreting Von Laue in terms of constructive and destructive interference
- Moseley (1914) first measurement of a technological material (brass)
- W.W.I to W.W.II many developments in electron optics, crystal spectrometry, detectors
- Castaing using a focused beam using electrostatic lenses (PhD thesis 1951) and developed the first theoretical basis for the matrix effects
- commercialization rapidly followed
Electron Sample Interactions :
- a small pre-selected area of a solid specimen is bombarded with electrons
- volume approx. several cubic micrometers in think polished sections (TPS)
- down to 104 atom volume in thin specimens due to lack of scattering :
- backscattered primary electrons
- low energy photo-electrons (secondary) and Auger electrons
- characteristic x-ray emission
- continuous background spectra (Bremsstrahlung)
- photo-emission (cathodo-luminescence) in transparent specimens (color)
- electron induced currents in semi-conductors or simply absorbed current
- transmitted electrons in thin specimens (EELS or electron energy loss spectrometry)
- thermal energy (heat)
Production of X-rays :
- continuum from slowing of electrons from (highest energy) :
where hc approx. = 12.4 (Planck's Constant times speed of light)
- continuum maximum peak at :
- characteristic x-rays from energy transferences involved in the re-arrangement of orbital electrons in the target element, followed by ejection of one or more electrons in the excitation process :
- Ka = Ek < El
- Kb1 = Ek < Em
- La = El < Em- non-diagram lines (simultaneous excitations)
- Auger (non radiative)
Measurement of Intensities :
-measurement precision (10K counts = 1 % precision)
-deadtime (1msec @ 10K cps = 1 % correction)
-beam current drift (< 1 % per hour w/ current regulation)
Corrections to Data :
- background correction (P/B of 10:1 = 10 % @ 10 % precision = 1 %)
Linear Slope Calculation
![]()
Exponential Slope Calculation
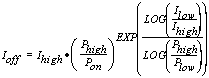
where :
= the off-peak count correction
= the x-ray counts for the high off-peak position
= the x-ray counts for the low off-peak position
= the high off-peak position
= the low off-peak position
= the on peak position
- accuracy of standards (gravimetric < 1 - 5 %)
- spectral interferences (typically 0.01 to >10 %)
O ka by Na = 30 %
Na ka by Zn = 5 %
Cl ka by Mo = 100 %
Cr ka by V = 2 %
As la by Fe = 2 %
Pd la by Rh = 20 %
- ZAF corrections (typically 10 to 100 %)
F ka by O = 300 % to 500 %
Si ka by Al = 34 % to 73 %
Al ka by Mg = 53 % to 211 %
Mg ka by Fe = 54 % to 96 %
where :
is the concentration of element A in the unknown
is the standard k-factor
is the ZAF correction factor for the unknown (iterated)
is the unknown k-ratio
Other Corrections :
- APF (Area-Peak-Factor) Correction
where :
= integrated intensity of unknown
= peak intensity of unknown
= peak intensity of standard
= integrated intensity of standard
- Volatile Alkali Correction
- use a linear fit of Log count intensity vs. time (assuming alkali loss is exponential)
- apply similar correction for refractory elements that increase in intensity
- recalculate matrix correction after adjustment to matrix
Sample Statistics:
-The range of homogeneity in plus or minus weight percent.
-The level of homogeneity in plus or minus percent of the concentration.
-The trace element detection limit in weight percent.
-The analytical sensitivity in weight percent.
where :
C is the actual concentration in weight percent of the sample
Cs is the actual concentration in weight percent of the standard
is the Student t for a 1-a confidence and n-1 degrees of freedom
n is the number of data points acquired
is the standard deviation of the measured values
is the average number of counts on the unknown
is the continuum background counts on the unknown
is the average number of counts on the standard
is the continuum background counts on the standard
![]()
Where :
= specimen absorbed current (mA)
= accelerating voltage (kV)
= thermal conductivity (cal cm-1 sec-1 deg-1)
= electron probe diameter (mm)
or
![]()
Where :
= electron beam in KeV
= thermal conductivity in watts cm-1 K-1-1
= beam diameter in um (microns)
= beam current in uA
Typical k values :
obsidian glass 0.014
zircon 0.042
quartz 0.10
calcite 0.05
iron metal 0.80
epoxy 0.002
| pixel density | number of pixels | .1 sec/pixel | 1 sec/pixel | 10 sec/pixel | 100 sec/pixel |
| 16 X 16 | 256 | 25.6 sec | 4.2 min | 42 min | 7.1 hrs |
| 64 X 64 | 4096 | 6.8 min | 68 min | 11.3 hrs | 4.7 days |
| 128 X 128 | 16384 | 27.3 min | 4.5 hrs | 1.9 days | 18.9 days |
| 256 X 256 | 65536 | 1.82 hrs | 18.2 hrs | 7.58 days | 75.8 days |
| 1024 X 1024 | 1048576 | 29.1 hrs | 12.1 days | 121.3 days | 3.3 years |
Back To Department of Earth and Planetary Science Home Page