TECHNICAL NOTE #1
High (or low) Totals in Inhomogenous Samples
From time to time you may have observed a situation where the analysis of certain samples produces an unexpectedly high (or low) total. Assuming that all other possible problems have been ruled out (including noisy electronics, low totals on a standard used in the calibration, an interference not corrected for or possibly porous samples), the next cause to consider is sample inhomogeneity.
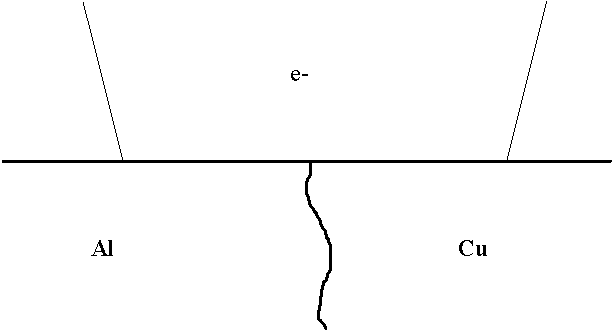
Consider the extreme situation depicted below. An interface of Al and Cu metal where the electron beam excites x-rays from both sides of the interface.

In this situation, x-rays of both metals will be produced. However, note that because the Cu x-rays are generated mostly in a pure Cu matrix and the Al x-rays are mostly generated in an pure Al matrix, the actual matrix correction that needs to be applied to the measured x-rays will be different than simply the matrix correction for a homogenous alloy sample consisting of both Al and Cu.
Now, as you may know, the matrix correction for the x-ray of an element in the pure element is considered to be 1.0. Hence for the majority of the x-rays produced in this sample, the matrix correction that needs to be applied to each x-ray is very close to 1.0 since, as stated above, most of the Cu x-rays are generated in a pure Cu matrix and most of the Al x-rays are generated in a pure Al matrix. However, when the microprobe measures the x-ray intensities at this boundary and receives both Al and Cu x-rays, it knows nothing of the actual geometry, and can only assume that all the x-rays measured are to be matrix corrected using a composition that is determined by iteratively correcting the measured x-ray intensities. This is the nature of the ZAF or Phi-Rho-Z matrix correction. Of course, one could apply a geometric model to the matrix correction to correct for the interface effect, but this would require precise knowledge of the interface shape and orientation which is usually not available.
Since determining the geometry of a buried interface is difficult if not impossible, the software can only assume a matrix correction based on a composition consisting of both Cu and Al, since both x-rays were detected. The matrix correction for Al x-rays in a homogenous Cu-Al alloy is of course quite different than that of pure Al, which is really the situation that created the Al x-rays in our example and the same is true for the Cu x-rays as well. The effect of assuming a homogenous matrix, when in fact the sample is very inhomogenous, is to apply the wrong matrix correction to the x-rays detected from the sample.
The following is a calculation for the correction of Cu ka and Al ka x-rays in a 50:50 homogenous alloy at 15kV and a 52.5 degrees takeoff angle :
| 50:50 Cu-Al alloy | Cu | Al |
| Elemental k-ratio | 0.45732 | 0.34037 |
| ZAF correction | 1.0933 | 1.4690 |
As you can see, the correction for both x-rays, but especially Al ka (47% ZAF correction), is significantly higher than the correction for each x-ray in the pure element (1.0). This will result in a very high total as the beam straddles the interface between the two phases, since both x-rays will be over corrected by homogenous alloy composition matrix correction. This example is extreme, but the situation applies to any inhomogenous sample in which the matrix correction for the different phases present are not equal. This is because the matrix correction itself is non-linear and cannot be applied to the normalized x-ray intensities generated from the different phases.
It is best to remember the words of the late Chuck Fiori, who said : "if the feature is smaller than the size of the beam, then all bets are off".
It is also important to remember that when the sample inhomogeneity is much smaller than the scale of the beam (for example particle phases less than 0.05 microns), that this effect becomes insignificant due to the fact that the many phases involved in the production and absorption of the x-rays tend to average out the contribution from a single phase. Of course this also means that it is possible to only determine the average composition of very fine grained materials. But at least we don't have to worry about inhomogeneity on the atomic scale!