
Using Quantitative Iteration to Correct "Pathological" Spectral Interferences
Microscopy & Microanalysis, Atlanta, Georgia, July
12-16, 1998
Problem Elements and Spectrometry Problems Symposia
By John J. Donovan
Department of Geology and Geophysics, University of California,
Berkeley, CA
As microanalysts, working in what is commonly considered to be a "mature" field, we would like to imagine that it is possible to quantitatively analyze any sample that happens to drop into our laps, however, as we have already seen this morning, that belief is not always in accordance with reality.
For the next 30 minutes, I would like to talk about two types of spectral interferences, both of which I like to term "pathological", due to the degree of difficulty they present to the analyst, although I should mention that the methods to be described here are completely applicable to the more frequently encountered and much less difficult cases of minor spectral overlap.
Cascade
Although these two types of "pathological"
interferences are related and can be treated similarly, I
designate the first type as "cascade" overlaps,

where element A interferes with element B, which in turn interferes with element C. The difficulty here of course is that one cannot correct for the interference on element C until one determines the interfering intensity contributed from element B, and one cannot determine the actual intensity contribution of element B on element C until one has determined the contribution of the interfering intensity from element A on element B.
"Self-interfering"
And the second type I designate "self-interfering"
overlaps

where two primary analytical lines both interfere significantly with each other. In this case the difficulty is that since both lines are first order diffraction peaks and hence of similar energy, we cannot take advantage of pulse-height analysis (PHA) to suppress the interference, and for various other analytical reasons we might not be able to switch to an alternative emission line that avoids the interference altogether.
Of course, one can conceive of yet another type of "pathological" overlap which might consist of simultaneous "cascade" and "self-interfering" overlaps.

Although I was unable to obtain a sample that demonstrates this extreme situation, it is not altogether impossible that one could encounter such a specimen. In any case, I did some quick overlap calculations on a hypothetical composition of this type and the results can be seen in the following figure.
Table 1
For As ka LiF at 1.17728 wt. %: 33.000 Interference by Bi LA2 at 1.15560 = .2% Interference by Pb SLAA at 1.16710 = .3% Interference by Pb SLAA at 1.16790 = .3% Interference by Pb SLAA at 1.16940 = .4% Interference by Pb SLA at 1.17070 = .5% Interference by Pb SLA^IX at 1.17150 = .5% Interference by Pb SLA^Y at 1.17300 = .6% Interference by Pb LA1 at 1.17520 = 64.5% Interference by Pb SLA1^Z at 1.17570 = .7% Interference by Pb SLAS at 1.18230 = .5% Interference by Pb LA2 at 1.18660 = 3.8% For Pb la LiF at 1.17518 wt. %: 33.000 Interference by Bi SLAA at 1.13520 = .1% Interference by Bi SLA^X at 1.13910 = .2% Interference by Bi SLA^IX at 1.14050 = .2% Interference by Bi SLA' at 1.14180 = .2% Interference by Bi LA1 at 1.14410 = 25.5% Interference by Bi SLA1^Z at 1.14450 = .3% Interference by Bi SLAS at 1.15150 = .5% Interference by Bi LA2 at 1.15560 = 6.6% Interference by As SKA4 at 1.17050 = 1.0% Interference by As SKA3' at 1.17140 = 1.0% Interference by As SKA3 at 1.17200 = 1.0% Interference by As KA1 at 1.17610 = 99.9% Interference by As KA1,2 at 1.17740 = 150.5% Interference by As KA2 at 1.18010 = 49.8% For Bi la LiF at 1.14402 wt. %: 33.000 Interference by Pb SLAA at 1.16710 = .5% Interference by Pb SLAA at 1.16790 = .4% Interference by Pb SLAA at 1.16940 = .4% Interference by As SKA4 at 1.17050 = .4% Interference by Pb SLA at 1.17070 = .4% Interference by As SKA3' at 1.17140 = .3% Interference by Pb SLA^IX at 1.17150 = .3% Interference by As SKA3 at 1.17200 = .3% Interference by Pb SLA^Y at 1.17300 = .3% Interference by Pb LA1 at 1.17520 = 25.2% Interference by Pb SLA1^Z at 1.17570 = .2% Interference by As KA1 at 1.17610 = 23.3% Interference by As KA1,2 at 1.17740 = 31.3% Interference by As KA2 at 1.18010 = 8.2% Interference by Pb SLAS at 1.18230 = .1% Interference by Pb LA2 at 1.18660 = .9%
Here we have As, Pb and Bi each assumed present at 33% weight percent concentration in just such a compound. As you can see, not only are Pb and As both interfering with each other, but Bi interferes with Pb which also "self-interferes with Bi" which in turn is interfered by both As and Pb. It's almost obscene!
However, not to worry just yet, I was unable to find a Pb-As-Bi sulfide in quick look through a mineralogy text, which doesn’t preclude the possibility of a synthetic material of course!
Benitoite
Now let's take a quick look at a more typical and benign
"self-interfering" overlap, for example Ba la and Ti ka as in
the mineral Benitoite.
Fig (4) Benitoite EDS spectra

As you can see in this EDS spectra of Benitoite, although acquired at the highest pulse processing time of my system, the detector is unable to separate the Ba la and Ti ka analytical peaks. However, the situation for the WDS acquired spectra is significantly improved using an LiF analyzing crystal under the same conditions.
Fig (5) Benitoite WDS spectra
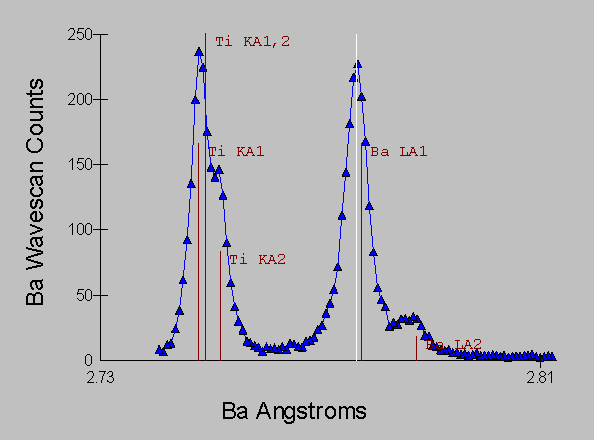
and it is obvious that only a small amount of overlap from the peak tails is occurring.
Polygonization
Incidentally, one significant source of interferences in
WDS, especially when measuring trace element concentrations, are
these rather extended tails that one can detect to a great
distance from the nominal emission line position. Although small
in intensity, these extremely extended tails, are an artifact of
the analyzer crystals used in electron microprobes. This artifact
is the result of the "polygonization" process that the
analyzing crystals undergo during manufacture.
Fig. (6) "Polygonization"
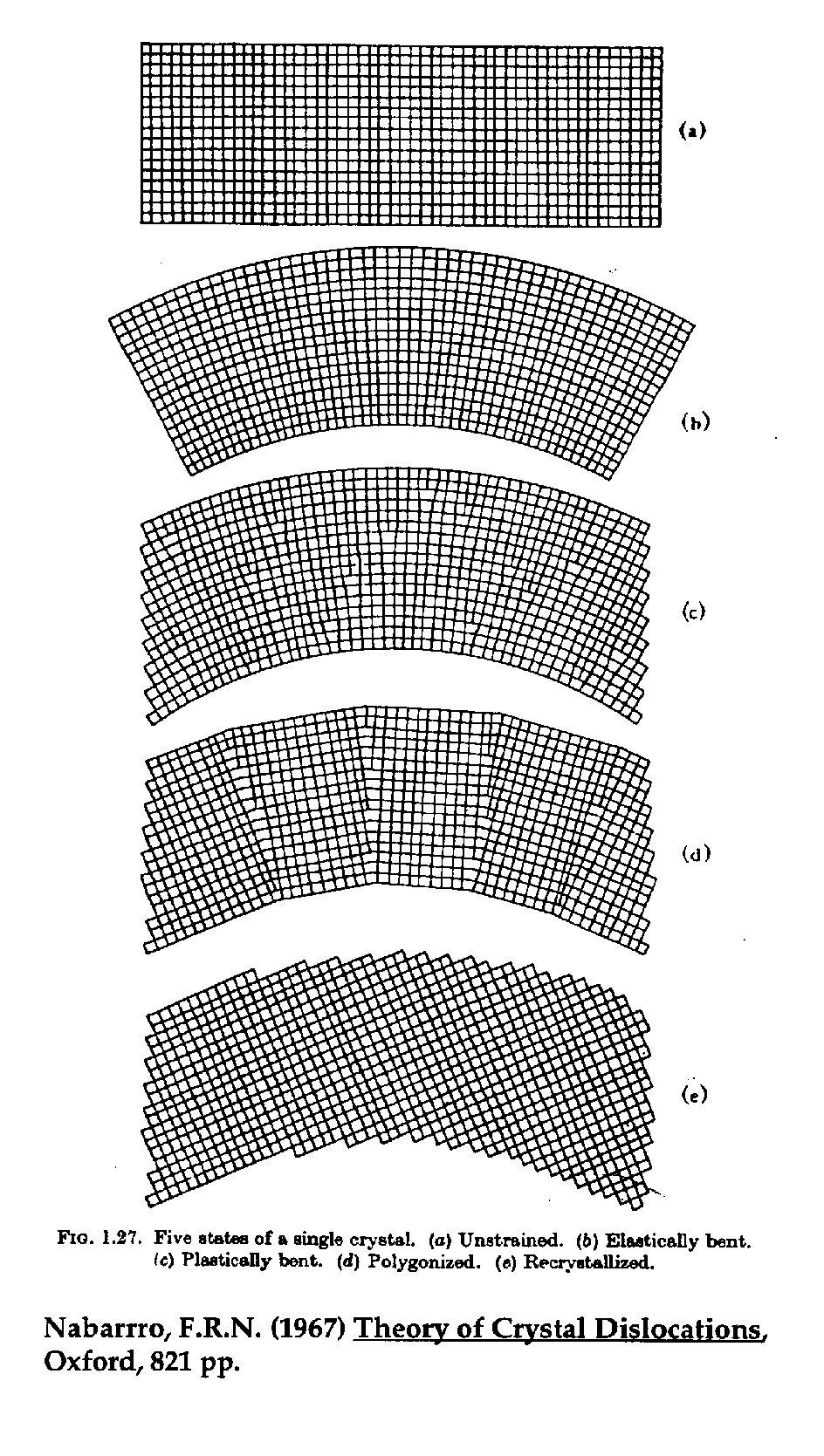
It turns out that freshly bent analyzing crystals are particularly poor in their ability to diffract x-rays due to plastic deformation that occurs when the crystals are curved to the Johann radius. To restore "reflectivity", the crystals are thermally cycled in order to partially recrystallize them, thus forming short polygon crystalline segments (and hence the term "polygonization"). However, one side effect of this process is that a certain amount of randomization is induced during the formation of these newly crystallized regions and in fact, although most segments will align themselves to the general curve of the crystal, a small fraction of them are misoriented at large angles, enough to cause x-ray diffraction at spectrometer positions far from the expected sinq angle.
Because of polygonization induced tailing, it is best to keep in mind the words of Chuck Fiori who once said "at a sufficiently trace level, every element in the periodic table interferes with every other element in the periodic table".
Large Magnitude Self-Interfering Overlaps
Some slightly more terrifying examples of
"self-interfering" overlaps can be easily found and the
following is a partial list of binary pairs for large magnitude
interferences of this type, calculated by assuming typical
wavelength dispersive resolution, that were gleaned from a quick
examination of the periodic table.
Table (2)
Interfering Pair |
Wavelength Region (Å) |
Approximate Overlap (% @ 50/50) |
Pb La « As Ka |
1.17 |
150 - 65 |
Hg La « Ge Ka |
1.25 |
120 - 15 |
Ir La « Ga Ka |
1.34 |
70 - 30 |
Re La « Zn Ka |
1.43 |
140 - 60 |
Er La « Co Ka |
1.78 |
110 - 50 |
Eu La « Mn Ka |
2.1 |
15 - 5 |
Ba La « Ti Ka |
2.7 |
0.8 - 0.8 |
Xe La « Sc Ka |
3.0 |
20 - 10 |
In La « K Ka |
3.74 |
50 - 20 |
Th Ma « Ag La |
4.13 |
30 - 60 |
Bi Ma « Tc La |
5.1 |
50 - 70 |
Mo La « S Ka |
5.4 |
30 - 15 |
Although I cannot claim to have personally encountered all of the above combinations (for instance, I doubt that a technetium-bismuth alloy will ever find it's way into my lab), I have run into more than a few of the others and, as I'm sure many of you already know, interferences of these magnitudes can be quite troublesome to deal with.
Just for comparison, I should point out that the previously discussed barium - titanium interference, also included here, is, as you can see, completely dwarfed in magnitude by the other examples in this table.
Self-interfering example
For the purposes of discussing interferences of this
variety, I will concentrate on the system Pb La
« As Ka
because the sulphosalt mineral family which commonly contains
these elements, is often encountered in ore petrology
investigations.
Let's take a quick look at some actual spectra from these types of samples, which exhibit, what I have already termed, overlaps of the "self interfering" variety. Here is an EDS spectra, of an unknown ore mineral, again acquired with a pulse processing time configured for maximum energy resolution.
Fig (7) ore mineral
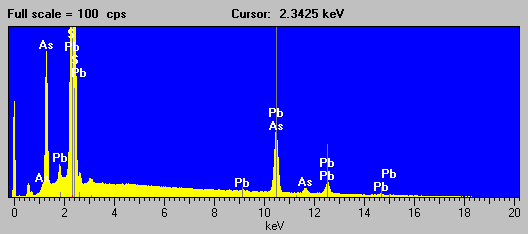
Not a very pretty picture, but it is at least evident that that As is present from the As La line and Pb likely present from the appearance of the secondary L lines, although S is interfered strongly by the Pb Ma line and can only be inferred by the mineralogy.
Here now we have the same ore mineral sample, and it's spectra acquired in the vicinity of the Pb La and As Ka lines, using a WD spectrometer equipped with an LiF analyzing crystal with an approximate energy equivalent resolution of 10 eV.
Fig (8)
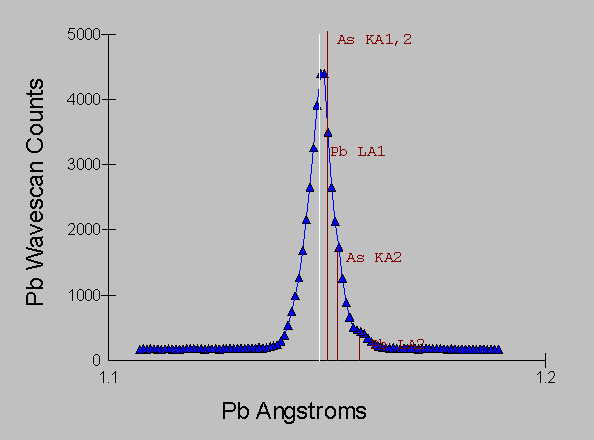
Even with the kind of resolution available with WDS, we still have large overlaps that will create confusion with qualitative analysis and much difficulty when we attempt quantitative analysis.
Cascade Example
The other "pathological" interference that can
also be extremely difficult for many analysts, are of course the
already mentioned "cascade" interferences. This is a
situation often, but not exclusively encountered in minor or
trace element analysis, in which, a major element will interfere
with another major or minor element, which in turn, interferes
with yet another minor or trace element. The difficulty is that
if one attempts to correct for the overlap on the trace element,
one must know the intensity of the interfering element, however,
if this interfering intensity has been significantly inflated by
yet another interference, one must correct for that interference
before correcting for the overlap on the trace element.
From this observation, we might surmise that the order in which the interferences are dealt with, could be important in the correction procedure, which is of course an undesirable restraint from a programmatic viewpoint.
Examples of this "cascade" interference, are readily found among the transition metals due to the Kb interferences that are ubiquitous in that region of the periodic table for the elements V to Cu, and also from a series of Lb interferences in the vicinity of Rh and Ag.
The following table contains some calculations regarding "cascade" overlaps for two different combinations of elements, again assuming typical WDS spectral resolution.
Table (3)
For V ka LiF at 2.50498 wt. %: 33.000 For Cr ka LiF at 2.29113 wt. %: 33.000 Interference by V SKB'' at 2.27680 = .1% Interference by V KB1 at 2.28490 = 6.5% Interference by V KB3 at 2.28490 = 3.3% Interference by V SKB' at 2.29040 = .7% For Mn ka LiF at 2.10326 wt. %: 33.000 Interference by Cr KB1 at 2.08510 = .7% Interference by Cr KB3 at 2.08510 = .3% Interference by Cr SKB' at 2.09000 = .2% Interference by Cr SKBN at 2.11770 = .1%
Table (4)
For Rh la PET at 4.59809 wt. %: 33.000 For Pd la PET at 4.36830 wt. %: 33.000 Interference by Rh SLB1^4 at 4.33610 = .2% Interference by Rh SLB1''' at 4.34420 = .4% Interference by Rh SLB1'' at 4.35180 = .7% Interference by Rh SLB1' at 4.36170 = .9% Interference by Rh LB1 at 4.37480 = 39.4% For Ag la PET at 4.15503 wt. %: 33.000 Interference by Pd SLB1''' at 4.11780 = .1% Interference by Rh SLB2^A at 4.12480 = .3% Interference by Pd SLB1'' at 4.12520 = .3% Interference by Rh LB2 at 4.13130 = 3.8% Interference by Pd SLB1' at 4.13510 = .6% Interference by Pd LB1 at 4.14650 = 38.8%
The V-Cr-Mn interference isn't too bad, at these particular concentrations, but if one were trying to measure a trace amount of Mn, it would be much more problematic. The Rh-Pd-Ag interference is extremely large and definitely requires special handling. Note that even these large concentrations experience overlaps of 30 to 40%.
In this talk I will examine two different real world examples of "cascade" interference, the first is an interesting interference caused by the fact that the K line of a higher Z transition metal is capable of fluorescing both the Ka and Kb lines of a slightly lower Z transition metal, which in turn can interfere with the trace analysis of another transition metal.
Here is the EDS spectra of a Fe-Ni alloy (NIST SRM 1159) that exhibits this "cascade" fluorescence interference.
Fig (9)
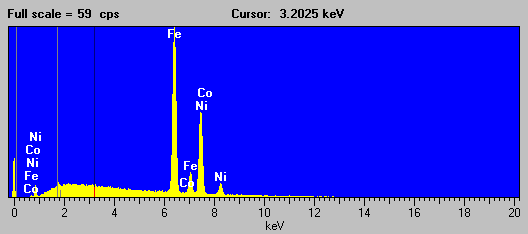
As you all know, the presence of Ni in the sample, causes a large fluorescence of both the Fe Ka and Kb lines, of which the Fe Kb line interferes with the Co Ka line sufficiently to cause problems when attempting to determine trace concentrations of Co in any Fe-Ni alloy. The bottom line here is: beware of any quoted Co trace concentrations in a matrix of Fe and Ni!
Fig (10)
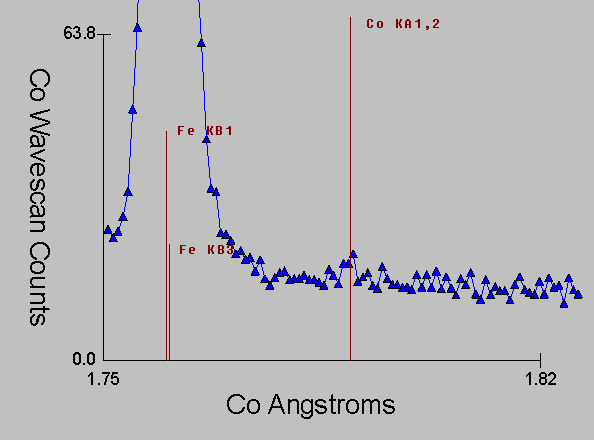
Again, here is the corresponding WDS spectra, which even with it's intrinsically higher resolution is unable to prevent the extended tails (and satellite lines) from the Fe Kb line from interfering with the Co Ka line.
And here is an EDS spectra of the second "cascade" interference example that I will discuss in a moment, a more typical, but still fascinating example of the perversity of the universe, in which the Kb lines of three consecutive transition metals each in turn strongly interferes with the next transition metal element in the periodic table, in this case a Ti-V-Al alloy (NIST SRM 654b) which has the interference Ti to V to Cr. (Ti Kb ® V Ka - V Kb ® Cr Ka):
Fig (11)
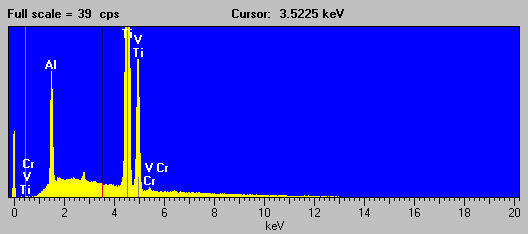
Fig (12)
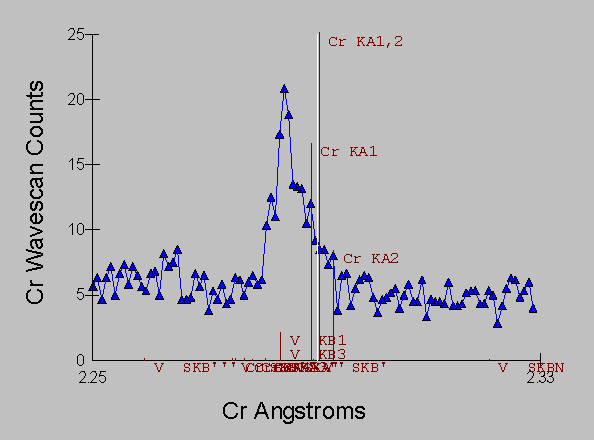
And corresponding the WDS spectra of the same sample which again, even with it's intrinsically higher resolution is incapable of separating the interference of V Kb ® Cr Ka:
Technique
What I would like to discuss now, is a general procedure that
can be used to deal with all types of "pathological"
(and of course, minor) spectral interferences. For this, I will
utilize wavelength dispersive data, since this represents the
best resolution currently available, and I will further restrict
the discussion to methods based on peak intensities, as opposed
to graphical methods working with complete spectra, which for WDS
spectrometers, are quite time consuming, especially for trace
element concentrations.
One procedure for the correction of spectral overlaps used by many analysts (typically as a "back-of-the-envelope" calculation), is based on a simple ratio of the interfering and interfered intensities.
This method will be completely inadequate for dealing with the types of interferences that we have been discussing. This can be easily understood by considering that in the case of "self-interfering" overlaps, the contribution to the interfering intensities must be solved simultaneously. A quick look at some actual measured intensities will show the magnitude of the problem:
Table (5)
| Pb La (cps) | As Ka (cps) | S Ka (cps) | |
| PbS | 1473.3 ± 11.5 | 1213.0 ± 3.8 | 1453.3 ± 9.3 |
| GaAs | 1624.7 ± 29.9 | 1771.7 ± 8.2 | 2.5 ± 1.2 |
| FeS | 14.0 ± 3.3 | 13.9 ± 3.7 | 4986.9 ± 26.3 |
As you can see here, the interfering intensity from As as measured in GaAs at the emission line position for Pb La, is actually greater than the intensity of Pb La as measured in PbS due to the greater relative strength of K lines compared to L lines!
Now let us examine the interference correction procedure itself. Here I will refer to a schematic diagram of a typical interference to explain the nomenclature
Fig (13)
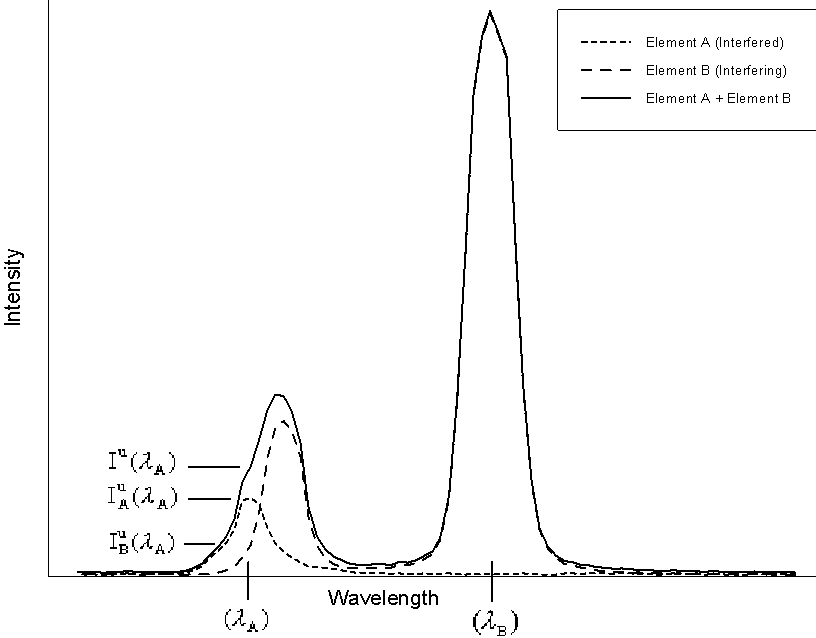
In this diagram, element A is the interfered element, whose
spectra is shown by the short dashed line, measured at it's
analytical line position, ![]() , element B is the
interfering element shown by the long dashed line, measured at
it's normal analytical line position,
, element B is the
interfering element shown by the long dashed line, measured at
it's normal analytical line position, ![]() ,
and the actual spectra, in a sample containing both
elements, as measured by the analyst, is shown by the solid line.
Therefore, the actual intensity of interfered element, is found
by subtracting the interfering intensity, contributed by the
interfering element from the overall measured intensity.
,
and the actual spectra, in a sample containing both
elements, as measured by the analyst, is shown by the solid line.
Therefore, the actual intensity of interfered element, is found
by subtracting the interfering intensity, contributed by the
interfering element from the overall measured intensity.
The expression seen here (e.g., Gilfrich, et al., 1978), for the determination of the interfering intensity contributed by element B, is often utilized,
Eq (1)
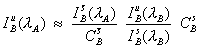
where the notation shown in the previous schematic, been adopted. What is being done here, is essentially calculating an approximate concentration for the presence of the interfering element in the unknown times it’s fractional overlap coefficient at the analytical position for the interfered element.
The interfering element intensity, is then, as noted before, simply subtracted from the measured intensity, to obtain the approximate intensity of the interfered element.
Shortcomings of the commonly utilized method
As previously mentioned, this procedure fails for the more
problematic "cascade" and "self-interfering"
spectral overlaps, where the intensity of the interfering element
is affected by an additional interference and even in cases of
minor overlap where differences in composition between the
unknown and the standard used for the interference calibration
may significantly affect the interfering intensity.
However, since in all cases of overlap, the degree of spectral interference is actually not directly dependent on the intensity of the interfering element, but is rather, compositionally dependent on the concentration of the interfering element, we can accurately determine the interfering intensity once we have accurately determined the concentration of the interfering element. Therefore, to perform a rigorous correction for interference, two important modifications to eq. (1) are required.
Improved Interference Correction
First, it is necessary to quantitatively correct for the
matrix effects on the interfering intensity in the interference
standard matrix relative to the unknown, as seen here,
Eq (2)
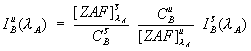
where the ZAF term is the ZAF or frz matrix correction factor for the element in the matrix. This not an entirely new idea, Myklebust included a correction for absorption with his overlap coefficient method in FRAME C.
Second, because the concentrations of elements will vary as the interference correction is applied, the full matrix adjusted interference correction expression shown above, must be enclosed inside an additional iteration loop to allow the interference correction to be recalculated after the concentration of each interfered element is subsequently determined.
Fig (15) Flow Chart of the iteration procedure
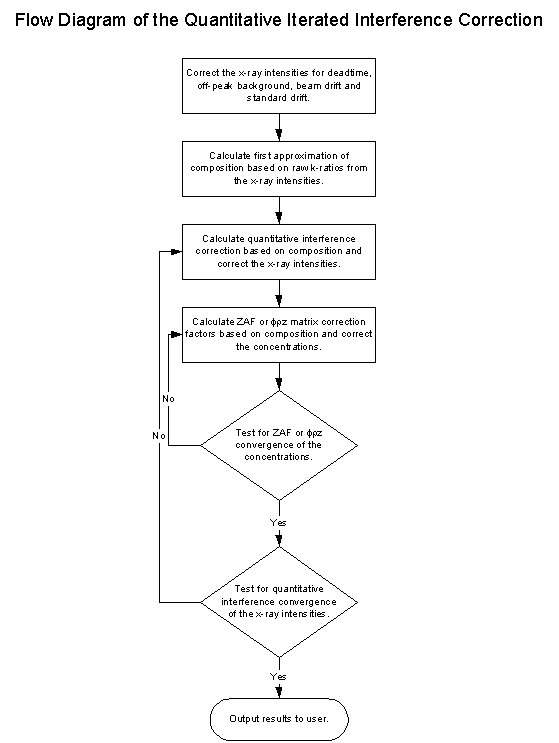
As you can see, this loop here is the typical ZAF or phi-rho-z iteration loop and surrounding it, the quantitative interference correction iteration loop.
It may seem at first, that the addition of an extra iteration loop is somewhat overkill for the calculation of the matrix effects of the interference correction, and in many cases it is, but it is exactly this additional iteration loop that allows us to not only calculate for "self interfering" overlaps, but also to correct for "cascade" overlaps without regard to the order of the interferences.
One small consideration is that this additional iteration loop would increase the number of computations by the square of the iterations, but thanks to Moore's Law, which posulates that the speed of microprocessors doubles every 18 months, we have absolutely no cause for concern there.
An Approximation
Eq (3)
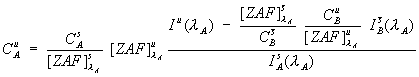 .
.
The full expression for the correction of interferences, along with the normal matrix correction for the concentration of the interfered element is shown here. As you can see, the term in the upper left, is the previously shown interference correction for the unknown intensity, after which the normal matrix correction procedure is applied.
However, there is one practical difficulty with eq. (3). It turns out that it is slightly difficult to estimate the fluorescence terms, here in the interference correction, because knowledge of the identity of all the excited lines would be required. Fortunately, except in some unusual cases, these fluorescence terms are generally near unity and can be neglected. Consequently, I have approximated equation (3) with
Eq. (4)
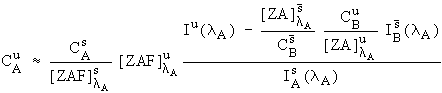 ,
,
and it is this expression that I will be using in the following data reductions.
Cascade Analyses
Starting with the "cascade" interferences, let's
perform some actual analyses on our old friends, the NBS SRM
alloys for which we have already seen some spectra for. In table
(6) we can see that equation (1), using the simple interfering
intensity ratio, significantly over estimates the interference
due to the secondary fluorescence of Fe Ka
by Ni and hence the interference of the trace quantity of Co in
the sample. On the other hand, eq. (2), using the quantitative
expression for the interfering element, produces a result which
calls to mind the phrase coined by Joe Michael of "spurious
accuracy".
And in the other case, the Ti to V to Cr (Ti Kb ® V Ka - V Kb ® Cr Ka) "cascade" interference in SRM 654b causes eq. (1) to actually calculate a "negative" concentration. On the other hand, equation (2) using the quantitative iteration, handles the situation quite reasonably.
Table (6), Analyses exhibiting interferences of the "cascade" variety.
wt. % (nominal) |
wt. % (uncorrected) |
wt. % (Eq. 1) |
wt. % (Eq. 2) |
|
| Ni K Þ Fe Ka Fe Kb ® Co Ka |
Co 0.022 1 | 0.089 ± 0.008 | 0.010 | 0.022 ± 0.008 |
| Ti Kb ® V Ka V Kb ® Cr Ka |
Cr 0.025 2 | 0.268 ± 0.01 | -0.020 | 0.021 ± 0.010 |
1 SRM 1159 includes : Ni 48.2, Fe 51.0, C 0.007, Mn 0.30, P 0.003, S 0.003, Si 0.32, Cu 0.038, Cr 0.06, Mo 0.01
2 SRM 654b includes : Ti 88.974, Al 6.34, V 4.31, Fe 0.23, Si 0.045, Ni 0.028, Sn 0.023, Cu 0.004, Mo 0.013, Zr 0.008
Self-Interfering Analyses
Table (7) Analyses exhibiting interferences of the
"self-interfering" variety.
wt. % (nominal) |
wt. % (uncorrected) |
wt. % (Eq. 1) |
wt. % (Eq. 2) |
|
| Ba La « Ti Ka (PET) |
Ba 33.15 3 Ti 11.69 |
33.26 ± 0.18 11.71 ± 0.08 |
33.08 11.59 |
33.08 ± 0.18 11.59 ± 0.08 |
| Pb La « As Ka | Pb 59.69 4 As 21.58 |
106.20 ± 0.33 41.38 ± 0.27 |
19.64 6.60 |
61.25 ± 1.97 22.15 ± 1.04 |
3 Benitoite (BaTiSi3O9) is assumed stoichiometric : Si 20.38, Ba 33.15, Ti 11.69, O 34.896
4 Shultenite (HAsPbO4) is assumed stoichiometric : Pb 59.69, As 21.58, O 18.44. The oxygen concentration was measured at 19.8 wt. % and included in the matrix correction calculations.
In the case of "self-interfering" interferences, we can see in table (7), that small interferences, such as the Ba La « Ti Ka system in the mineral Benitoite, are not difficult to deal with, even using equation (1). In fact, eq. (1) and (2) give exactly the same result within the precision of the analysis. This is because the matrix correction effect of the interfering line is negligible with this degree of overlap.
However, in the next example, a sample of Shultenite, with the ideal formulation HAsPbO4, which contains the Pb La « As Ka interference, the use of eq. (1) is obviously untenable, while equation (2) provides quite usable results in spite of a prolonged iteration procedure of approximately 50 iterations.
To show the difficulty of the convergence during the procedure, here in fig (16), I have graphed the change in the corrected intensity of Pb and As in the previously seen Shultenite calculation. As you can see, the iteration is extremely fierce but does eventually converge after some 50 or so iterations. Although I have not yet attempted it, it is likely that a hyperbolic iteration would converge somewhat more quickly.
Fig (16) Iteration of corrected intensities using the quantitative interference correction
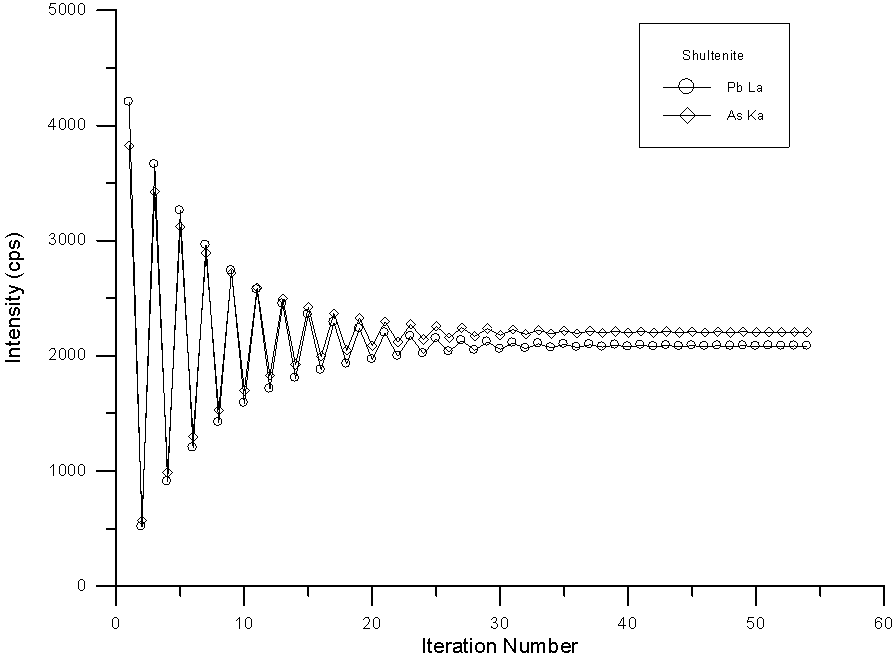
However, in spite of the instability of the iteration, the analysis is good enough to at least confirm the identification as shown the table (8), where the results and calculated formula based on 4 O atoms of the previous Shultenite analysis is shown.
Table (8) Shultenite HPbAsO4
Results in Elemental Weight Percents (Overlap Corrected)
Includes 0.312 H Calculated by Stoichiometry to O
ELEM: Pb As O SUM
20 63.283 21.132 20.129 104.861
21 59.046 23.467 19.811 102.636
22 60.169 22.475 19.583 102.535
23 62.504 21.539 19.624 103.977
AVER: 61.250 22.153 19.787 103.502
SDEV: 1.977 1.041 .249
Results Based on 4 Atoms of O
ELEM: Pb As O SUM
20 .971 .897 4.000 6.868
21 .921 1.012 4.000 6.933
22 .949 .980 4.000 6.929
23 .984 .938 4.000 6.921
AVER: .956 .957 4.000 6.913
SDEV: .028 .050 .000
Now, how well will this iteration technique work for the real world analysis of the previously mentioned sulphosalt ore minerals? For this, I obtained several specimens of Pb-As sulfides that were claimed to be Rathite, Jordanite, and Baumhauerite, each with a distinctive Pb-As ratio.
Table (9)
| Rathite | (PbS)3 (As2S3)2 |
| Jordanite | (PbS)4 (As2S3) |
| Baumhauerite | (PbS)4 (As2S3)3 |
Jordanite
I first performed qualitative analysis on the specimens and
from the acquired spectra, it was immediately apparent that the
Rathite specimen was only a simple Fe sulfide and was therefore
discarded. The Jordanite sample, however, gave the following
intriguing analysis after correcting for interference using eq.
(2).
Table (10) Jordanite (?) (PbS)4 (As2S3)
Results in Elemental Weight Percents (Overlap Corrected)
ELEM: Pb As S SUM
46 68.487 12.433 20.072 100.992
47 69.599 11.729 19.256 100.584
48 70.781 11.620 19.759 102.160
49 64.479 13.488 19.848 97.815
50 73.699 9.375 19.250 102.323
51 72.970 9.540 19.279 101.789
52 67.115 13.301 20.061 100.476
53 66.667 13.553 19.741 99.960
AVER: 69.225 11.880 19.658 100.762
SDEV: 3.177 1.671 .350
Results Based on 4 Atoms of Pb
ELEM: Pb As S SUM
46 4.000 2.008 7.575 13.583
47 4.000 1.864 7.151 13.015
48 4.000 1.816 7.215 13.031
49 4.000 2.314 7.956 14.270
50 4.000 1.407 6.751 12.158
51 4.000 1.446 6.829 12.275
52 4.000 2.192 7.726 13.918
53 4.000 2.249 7.654 13.902
AVER: 4.000 1.912 7.357 13.269
SDEV: .000 .348 .437
Since the ideal formula for Jordanite is 2 As and 7 S per 4 Pb atoms, the identification is reasonable, despite the obvious instability and resulting large standard deviations in the analysis.
Baumhauerite ?
The qualitative analysis of the alleged Baumhauerite was also
performed, and immediately, it was discovered that the sample was
just "slightly" inhomogeneous as seen in the following
backscatter image.
Fig (17) BSE 20 keV, 20 nA, 1000x

However, I decided to continue and attempt to analyze the region near the rim of the material, since it seemed to be somewhat more homogeneous than the rest of the sample and could possibly contain a high Z element such as Pb as indicated by the higher BSE intensity. For this I was rewarded by the following quite reasonable analysis.
Table (11) Baumhauerite (?) (PbS)4 (As2S3)3
Results in Elemental Weight Percents (Overlap Corrected) ELEM: Pb As S SUM 990 38.244 32.544 25.930 96.718 991 43.676 29.847 25.220 98.743 992 46.014 28.958 24.809 99.781 993 36.710 33.744 26.094 96.548 994 46.770 29.248 25.152 101.170 995 43.240 29.969 25.392 98.601 996 41.550 31.464 26.367 99.381 997 41.248 31.365 25.739 98.352 AVER: 42.182 30.892 25.588 98.662 SDEV: 3.501 1.682 .531 Based on 4 Pb atoms ELEM: Pb As S SUM 990 4.000 9.413 17.524 30.937 991 4.000 7.559 14.925 26.484 992 4.000 6.961 13.936 24.897 993 4.000 10.168 18.372 32.540 994 4.000 6.918 13.900 24.817 995 4.000 7.667 15.178 26.845 996 4.000 8.376 16.402 28.778 997 4.000 8.411 16.128 28.540 AVER: 4.000 8.184 15.796 27.980 SDEV: .000 1.152 1.617
However, something was still not quite right, as you can see by the formula calculation. Baumhauerite should have 6 As atoms and 13 S atoms for every 4 Pb atoms. On a hunch, I recalculated the formula based on 1 Pb atom as shown in this next table. Although the specimen is definitely not Baumhauerite, my money is on an identification of Sartorite, another Pb-As sulfide, which has an ideal formula of 2 As atoms and 4 S atoms per Pb atom.
Table (12) Sartorite (?!) (PbS) (As2S3)
Based on 1 Pb atoms ELEM: Pb As S SUM 990 1.000 2.353 4.381 7.734 991 1.000 1.890 3.731 6.621 992 1.000 1.740 3.484 6.224 993 1.000 2.542 4.593 8.135 994 1.000 1.729 3.475 6.204 995 1.000 1.917 3.794 6.711 996 1.000 2.094 4.100 7.195 997 1.000 2.103 4.032 7.135 AVER: 1.000 2.046 3.949 6.995 SDEV: .000 .288 .404
Timing
Finally, just in case anyone here has any doubts that
pathological interferences can happen to you, I would like to
share with you something that walked right into my lab only two
weeks ago. In fact, just after I had these slides made. Perfect
timing I must say.
Elemental Wt. % Total: 100.000 Average Total Oxygen: .000 Average Calcu. Oxygen: .000 Average Excess Oxygen: .000 Average Atomic Weight: 49.900 Average Atomic Number: 54.873 ELEM: Re Zn S O N C H XRAY: la ka ka ka ka ka ELWT: 65.850 7.706 15.119 1.886 4.954 4.248 .238 KFAC: .5426 .0847 .1091 .0047 .0104 .0067 .0024 ZCOR: 1.2135 .9102 1.3854 4.0163 4.7817 6.3580 .0000 ATWT: 17.647 5.882 23.529 5.882 17.647 17.647 11.765 On Peak Interferences for : St 17 Zn-ReSCN For Re la LiF at 1.43298 wt. %: 65.850 Interference by Zn SKA3 at 1.42990 = .1% Interference by Zn SKA' at 1.43050 = .1% Interference by Zn KA1 at 1.43550 = 11.1% Interference by Zn KA1,2 at 1.43680 = 15.8% Interference by Zn KA2 at 1.43930 = 4.4% For Zn ka LiF at 1.43652 wt. %: 7.706 Interference by Re SLA^X at 1.42690 = 2.8% Interference by Re SLA^IX at 1.42960 = 3.9% Interference by Re SLA' at 1.43020 = 4.2% Interference by Re LA1 at 1.43310 = 519.8% Interference by Re SLAS at 1.43800 = 5.6% Interference by Re LA2 at 1.44420 = 40.7% For S ka PET at 5.37386 wt. %: 15.119 For O ka NiCrBN at 24.0041 wt. %: 1.886 Interference by Zn LB1 II at 23.9800 = 34.7% Interference by Zn LA1 II at 24.5020 = 1.0% Interference by Zn LA2 II at 24.5020 = .1% For N ka NiCrBN at 32.1138 wt. %: 4.954 For C ka NiCrBN at 45.4269 wt. %: 4.248
As you can see from this nominal composition, the substance is some sort of an organic cyanide and according to the student it contains clusters of rhenium and sulfur atoms, ideally in the ratio of 6 rheniums to 9 sulfurs. However, the problem is that this substance also contains significant zinc, which not only interferes with the rhenium but is in turn interfered by the rhenium itself. A classic case of self interference, and as you can see from this calculation, the estimated interference will substantially affect the analysis.
Anyway, here is the analysis of the substance without any interference correction. As you can see the interference is indeed quite severe.
Un 10 Zn-ReSCN gr2
TakeOff = 40 KiloVolts = 20 Beam Current = 20 Beam Size = 0
Elemental Wt. % Total: 123.137 Average Total Oxygen: .000
Average Atomic Weight: 54.342 Average Atomic Number: 53.229
Average ZAF Iteration: 4.00 Average MAN Iteration: 2.00
Results in Elemental Weight Percents
SPEC: O N C H
TYPE: SPEC SPEC SPEC SPEC
AVER: 1.900 5.000 4.200 .200
SDEV: .000 .000 .000 .000
ELEM: Cs Fe Zn Re S Se SUM
53 .000 .000 19.463 74.142 17.309 .000 122.214
55 .000 .007 20.459 74.986 16.357 .000 123.108
56 .000 .019 19.578 75.195 17.997 .000 124.089
AVER: .000 .009 19.833 74.774 17.221 .000 123.137
SDEV: .000 .010 .545 .558 .824 .000
SERR: .000 .006 .314 .322 .476 .000
%RSD: .1 113.3 2.7 .7 4.8 .1
STDS: 834 730 660 575 730 660
STKF: .5968 .4279 .5007 1.0000 .4736 .5158
STCT: 627.1 3670.9 3712.9 3672.8 4423.1 1315.9
UNKF: .0000 .0001 .2103 .6516 .0947 .0000
UNCT: -2.7 .3 1559.2 2393.0 884.3 -3.2
UNBG: 11.6 28.0 67.3 61.5 6.6 64.0
ZCOR: 1.2061 .9201 .9433 1.1476 1.8189 1.0216
KRAW: -.0043 .0001 .4199 .6516 .1999 -.0024
PKBG: .77 1.01 24.18 40.00 135.89 .95
Results Based on 6 Atoms of re
SPEC: O N C H
TYPE: SPEC SPEC SPEC SPEC
AVER: 1.774 5.334 5.225 2.965
SDEV: .013 .040 .039 .022
ELEM: Cs Fe Zn Re S Se SUM
53 .000 .000 4.486 6.000 8.134 .000 34.048
55 .000 .002 4.663 6.000 7.600 .000 33.518
56 .000 .005 4.450 6.000 8.339 .000 34.005
AVER: .000 .002 4.533 6.000 8.025 .000 33.857
SDEV: .000 .003 .114 .000 .382 .000
SERR: .000 .001 .066 .000 .220 .000
%RSD: .8 113.2 2.5 .0 4.8 .8
And after utilizing the iterated quantitative interference correction, the results are almost acceptable, especially for an analysis performed by a student. As you can see the ratio of rhenium to sulfur is close to predicted.
Un 10 Zn-ReSCN gr2
TakeOff = 40 KiloVolts = 20 Beam Current = 20 Beam Size = 0
Elemental Wt. % Total: 101.134 Average Total Oxygen: .000
Average Atomic Weight: 50.129 Average Atomic Number: 54.345
Average ZAF Iteration: 4.00 Average MAN Iteration: 14.33
Results in Elemental Weight Percents
SPEC: O N C H
TYPE: SPEC SPEC SPEC SPEC
AVER: 1.900 5.000 4.200 .200
SDEV: .000 .000 .000 .000
ELEM: Cs Fe Zn Re S Se SUM
53 .000 .000 6.325 65.726 17.333 .000 100.683
55 .000 .007 7.471 65.113 16.343 .000 100.233
56 .000 .019 6.188 66.949 18.029 .000 102.486
AVER: .000 .009 6.661 65.929 17.235 .000 101.134
SDEV: .000 .010 .704 .935 .848 .000
SERR: .000 .006 .407 .540 .489 .000
%RSD: .1 113.3 10.6 1.4 4.9 .0
STDS: 834 730 660 575 730 660
STKF: .5968 .4279 .5007 1.0000 .4736 .5158
STCT: 627.1 3670.9 3712.9 3672.8 4423.1 1315.9
UNKF: .0000 .0001 .0704 .5727 .0947 .0000
UNCT: -2.7 .3 522.0 2103.2 884.3 -3.2
UNBG: 11.6 28.0 67.3 61.5 6.6 64.0
ZCOR: 1.2207 .9322 .9463 1.1513 1.8203 1.0207
KRAW: -.0043 .0001 .1406 .5727 .1999 -.0024
PKBG: .77 1.01 8.75 35.26 135.89 .95
INT%: .00 .00 -66.57 -12.11 .00 .00
Results Based on 6 Atoms of re
SPEC: O N C H
TYPE: SPEC SPEC SPEC SPEC
AVER: 2.013 6.050 5.926 3.363
SDEV: .028 .085 .084 .047
ELEM: Cs Fe Zn Re S Se SUM
53 .000 .000 1.645 6.000 9.189 .000 34.236
55 .000 .002 1.961 6.000 8.745 .000 34.274
56 .000 .006 1.580 6.000 9.383 .000 34.053
AVER: .000 .003 1.728 6.000 9.106 .000 34.188
SDEV: .000 .003 .204 .000 .327 .000
SERR: .000 .002 .118 .000 .189 .000
%RSD: 1.3 112.3 11.8 .0 3.6 1.4
Final slide (Escher)
In conclusion, I’d just like to say that, the use of a
quantitatively iterated interference correction is an essential
tool for WDS microanalysis. Because implementation of this
algorithm is simple, it is desirable that this capability be
available to the general EPMA community, not only for situations
involving extreme and multiple overlaps, but even for the less
severe and and more commonly encountered cases of minor spectral
interferences.
References
J. V. Gilfrich, L. S. Birks, J. W. Criss,
"Correction for Line Interferences in Wavelength-Dispersive
X-ray Analysis", in: X-Ray Fluorescence Analysis of
Environmental Samples, T. G. Dzubay Ed., Ann Arbor Science
Publ., Ann Arbor, (1978), 283.
J. J. Donovan, D. A. Snyder, M. L. Rivers, "An Improved Interference Correction for Trace Element Analysis", in: Microbeam Analysis, (1993), 2, 23.
Philibert J, Tixier R. Quantitative Electron Probe Microanalysis, In: NBS Special Publication, Ed. KFJ Heinrich. Washington, D.C., 1968, p. 13.
Myklebust, R. L., Fiori, C. E., and Heinrich, K. F. J., National Bureau of Standards Tech. Note 1106, 1979.
J. J. Donovan (1998) Using Quantitative Iteration to Correct for Pathological Spectral Interferences, in: Proc. Microbeam Analysis Society, San Francisco Press, San Francisco (in press)