This calculation of sample detection limits for non-replicate data (i.e., results quoted for a single measurement) is based on the standard counts, the unknown background counts and the magnitude of the ZAF correction factor. The calculation is adapted from Love and Scott (1974). This detection limit calculation is useful in that it can be used even on inhomogeneous samples and can be quoted as the detection limit in weight percent for a single analysis line with a confidence of 99% (assumes 3 standard deviations).
Where :
ZAF is the ZAF correction factor for the sample matrix
is the count rate on the analytical (pure element) standard
is the background count rate on the unknown sample
t is the counting time on the unknown sample
A fairly rigorous calculation of analytical error, also for single measurements, can be performed based on the peak and background count rates (Love and Scott, 1974). The results of the calculation can be displayed after multiplication by a factor of 100 to give a percent analytical error of the x-ray intensity. This analytical error result can be compared to the percent relative standard deviation (i.e., the count standard deviation divided by the average counts times 100). The analytical error calculation is as follows:
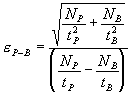
Where :
is the total peak counts
is the total background counts
is the peak count time
is the background count time
A more comprehensive set of calculations for detection limit and analytical sensitivity can be performed on replicate data (i.e., data for which multiple measurements are available and where the average is quoted). These statistics are based on equations adapted from "Scanning Electron Microscopy and X-Ray Microanalysis" by Goldstein, et. al. (Plenum Press, 1992 ed., 1981) p. 432 - 436. All calculations may be expressed for various confidence intervals from 60 to 99 % confidence utilizing appropriate values for Student's "t".
The calculations are based on the number of data points acquired in the sample and the measured standard deviation for each element. This is important because although x-ray counts theoretically have a standard deviation equal to square root of the mean, the actual standard deviation is usually larger due to variability of instrument drift, x-ray focusing errors, electronic noise and x-ray production. It is critical to evaluate sample homogeneity before considering analytical and sample detection limits.
The statistical calculations include :
1. The range of homogeneity in plus or minus weight percent.
![]()
2. The level of homogeneity in plus or minus percent of the concentration.
![]()
3. The trace element detection limit in weight percent.
![]()
4. The analytical sensitivity in weight percent.
Where :
is the concentration to be compared with
C is the actual concentration in weight percent of the sample
Cs is the actual concentration in weight percent of the standard
is the Student's "t" for a 1-a confidence and n-1 degrees of freedom
n is the number of data points acquired
is the standard deviation of the measured values
is the average number of counts on the unknown
is the continuum background counts on the unknown
is the average number of counts on the standard
is the continuum background counts on the standard
The homogeneity test merely compares the 99 % confidence range of homogeneity value with 1 % of the sample concentration for each element. If the range of homogeneity is less than 1 % of the sample concentration then the sample may be considered to be homogenous within 1 %.
The detection limit calculation here is intended only for use with homogenous samples since the calculation includes the actual standard deviation of the measured counts. This detection limit can, however, be quoted for the sample average and of course will improve as the number of data points acquired increases. Note that the homogenous sample detection limit calculation should be ignored for those elements which occur as minor or major concentrations (> 1 %). Conversely, the analytical sensitivity calculation should be ignored for elements whose concentrations are present at less than 1%.