Some Notes on the "Bence-Albee After 20 Years" paper by John Armstrong
As noted by John Armstrong and many others, the Bence-Albee matrix correction method was phenomenally popular in its day and remains useful today in modified form when high speed matrix calculations are required (e.g., quantitative imaging). As noted in the Armstrong paper linked here, the original method developed at Cal Tech was based on the Ziebold-Ogilvie form of the hyperbolic relationship between concentration and x-ray intensity shown here:
C/K = a + (1 - a) * C
where C = concentration, K = x-ray intensity (normalized to the pure element) and a = the correction factor for fluorescence, absorption and atomic number effects. This relationship was utilized at Cal Tech by assuming a single (constant) correction term for the full range of the binary composition by assuming a value at the 50:50 composition for ease of calculation. Since most silicate and oxide minerals are composed of major element concentrations this was a reasonable approximation for the use of slide rules at the time. A good introduction to this original formulation is found here on James Wittke's pages
Mark Rivers at UC Berkeley showed that this Ziebold-Ogilvie form of the expression can be solved for alpha by re-arranging the terms as shown below and in the early 1980s a linear (two coefficient) polynomial fit was developed by Mark and utilized at UC Berkeley on the PDP-11 equipped ARL SEMQ EPMA by myself and the graduate students there. This two coefficient expression very adequately accounts for matrix correction effects except in cases of very extreme fluorescence and absorption where the effects are even more non-linear.
a = (C/K - C)/ (1 - C)
This simplified expression, though never formally published by Mark, allows for the relationship between concentration and intensity to be modeled by any mathematical expression. Eventually John Armstrong utilized a polynomial three coefficient fit that handled even those cases of extreme fluorescence and absorption, and this improved method was subsequently published by Armstrong in 1988 in the Microbeam Analysis Proceeding in his "Bence-Albee After 20 Years" paper (please note the typo in the Armstrong paper for this expression, which is corrected by hand in the scanned paper linked above, i.e., equation 4 on page 470).
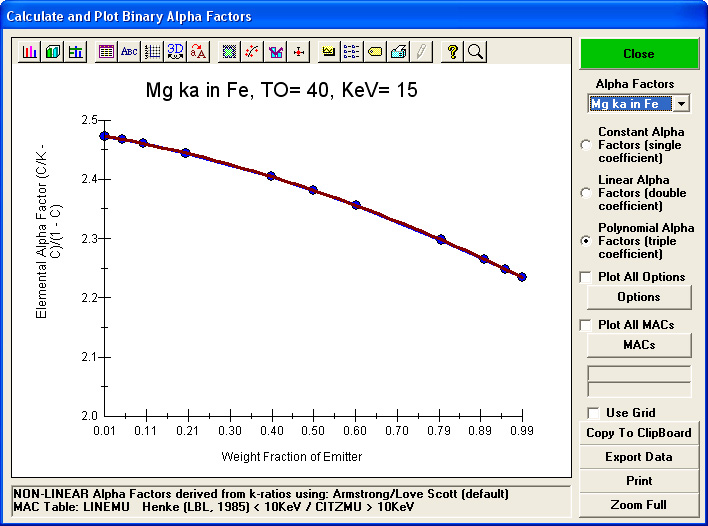
As described in Armstrong's paper this polynomial fit to the River's modified hyperbolic relationship can be used to fit intensities calculated from any general matrix correction method to create binary pure element alpha factors and compound beta factors for an arbitrary composition. These factors are easily calculated and output graphically or to a file using my CalcZAF utility program which can be downloaded for free from this link here.
An example of the graphical output generated during these CalcZAF calculations is shown here:

John Donovan
(541) 346-4632